On the Estimations of Bounds for Determinant of Hadamard Product of H-Matices
Keywords:
$H$-matrix, Determinant, Hadamard product.Abstract
In this paper, some estimations of bounds for determinant of Hadamard product of $H$-matrices are given. The main result is the following if $A = (a_{ij})$ and $B=(b_{ij})$ are nonsingular $H$-matrices of order $n$ and $∏^n_{i=1}a_{ii}b_{ii} > 0,$ and $A_k$ and $B_k, k=1, 2, \cdots, n,$ are the $k \times k$ leading principal submatrices of $A$ and $B$, respectively, then
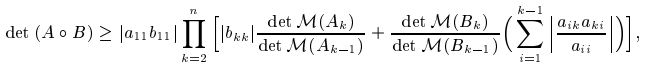
where $M(A_k)$ denotes the comparison matrix of $A_k$.
