Time Decay Estimates for Fourth-Order Schrödinger Operators in Dimension Three
DOI:
https://doi.org/10.4208/aam.OA-2024-0018Keywords:
Fourth order Schrödinger equation, asymptotic expansions, $L^1−L^∞$ decay estimate, resonances.Abstract
This paper is concerned with the time decay estimates of the fourth
order Schrödinger operator $H = ∆^2+V (x)$ in dimension three, where $V (x)$ is
a real valued decaying potential. Assume that zero is a regular point or the
first kind resonance of $H,$ and $H$ has no positive eigenvalues, we established the
following time optimal decay estimates of $e^{−it H}$ with a regular term $H^{α/4}:$
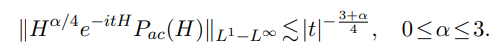
When zero is the second or third kind resonance of $H,$ their decay will be
significantly changed. We remark that such improved time decay estimates
with the extra regular term $H^{α/4}$ will be interesting in the well-posedness and
scattering of nonlinear fourth order Schrödinger equations with potentials.
