The $H^p-H^q$ Estimates for a Class of Dispersive Equations with Finite Type Geometry
DOI:
https://doi.org/10.4208/aam.OA-2025-0001Keywords:
Dispersive equations, $H^p-H^q$ estimates, finite type geometry, decay estimates.Abstract
This paper studies the $H^p-H^q$ estimates of a class of oscillatory
integrals related to dispersive equations
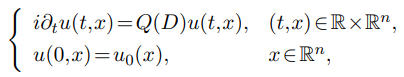
under the assumption that the level hypersurfaces are convex and of finite type.
As applications, we obtain the decay estimates for the solutions of higher order
homogeneous and inhomogeneous Schrödinger equations.
