Trudinger-Moser Type Inequality Under Lorentz-Sobolev Norms Constraint

Abstract

In this paper, we are concerned with a sharp fractional Trudinger-Moser type inequality in bounded intervals of R under the Lorentz-Sobolev norms constraint. For any $1

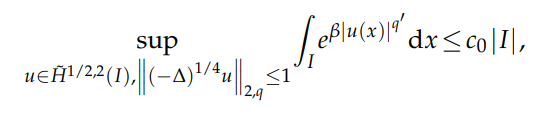
and $β_q$ is optimal in the sense that

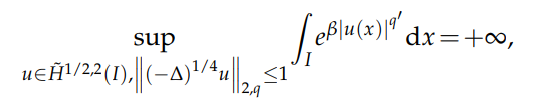
for any $β>β_q$. Furthermore, when $q$ is even, we obtain

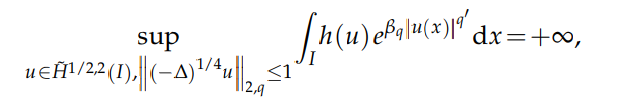
for any function $h : [0,∞)→[0,∞)$ with lim$_{t→∞} h(t) = ∞$. As for the key tools of proof, we use Green functions for fractional Laplace operators and the rearrangement of a convolution to the rearrangement of the convoluted functions.